AE制作逼真的弹跳和缓冲效果

　　有时你可能想美化您的动画动作有位物理真实感。例如，你可能有一个快速层从零扩展到100%，并要加一点过冲和振荡，有它最终定居在100%。另一个例子是，如果你有一个对象落入框架，你想，当它击中了底部反弹了一点。这两种情况看起来相似，但它们代表了完全不同的物理过程。任一这些模拟可以使用表达式来创建，但选择正确的一方面，这是很重要的。在这篇文章中，我将详细讨论这些动画工具以及就如何以及何时使用它们的一些技巧。

　　在这两个弹跳和缓冲的情况，你正在处理的衰减幅度。过冲，你一般都处理一个谐波振荡，就像你有一个摆或弹簧。这意味着频率保持不变(在对象的共振频率)作为振幅衰减。这通常是用模拟的指数衰减正弦波。这是一个简单的解决办法，但肯定是有窍门能让初始幅度正确匹配与传入的动画)。

　　

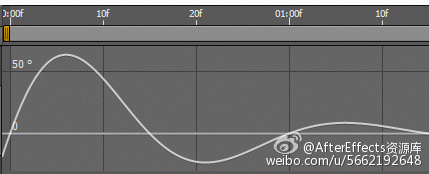
　　基本衰减的正弦波振荡应用到旋转属性。反弹是一个完全不同的野兽。当一个对象的反弹，它失去在每个反弹，这会影响二者的幅度和频率的能量。作为反弹的幅度降低，它们发生更频繁。这意味着正弦波模拟不足以反弹。事实上，反弹的波形实际上是一系列降幅的抛物线。物体停止在反弹的顶部，然后加速(由于一些重力状现象的力)，因此所涉及的数学运算是完全不同的。

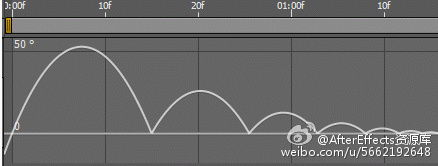
　　该波形通过模拟反弹表达式生成。请注意，反弹出现较多的对象失去能量。一个基本的反弹表达已应用到旋转属性。

　　缓冲详情

　　看一看基本表达式为指数衰减正弦波：

　　amp = 80;

　　freq = 1;

　　decay = 1;t = time - inPoint;

　　amp*Math.sin(t*freq*Math.PI*2)/Math.exp(t*decay);

　　因为它位于，这种表达会引发衰减的正弦波振荡图层的入点。前三行只需设定的波形参数进行：80最大振幅，每秒一个振荡的频率，和一个衰减(多快的振幅减小)之一值。变量t是用来计算由于层的In点的时间。所有真正的数学发生在最后一行。

　　注：

　　JavaScript函数Math.sin()和Math.cos()实现都产生正弦波，但他们的目的不同表达作家。该Math.sin()函数从零开始，增加价值。 Math.cos()实现为90度的相位差Math.sin()，这意味着它开始于最大值和减小。

　　你通常会选择Math.cos()实现当你想一开始就在完全伸展，或完全旋转状态的对象。例如，您可能要开始与摆在最高转速，而不是零钟摆运动。我们不会在这里使用它，但它是一个很好的工具来了解。

　　有三样东西，在最后一行回事。所述Math.sin()片产生频率频率而变化的正负之一之间振幅的正弦波。该Math.exp()件产生的曲线，在可变衰减所确定的速率成倍增加。正弦波得到由幅值变量(安培)相乘，并且该结果被由指数曲线的值除以，产生所希望的指数衰减正弦波。

　　这是一个方便的表达，有时是你所需要的。更多的时候，你会想用指数衰减正弦波提供一些振荡尖峰另一个运动结束。诀窍是让冲振荡的幅度，以进向速度相匹配。你做到这一点的方式取决于您的动画的性质。在某些情况下，可能必须即输入的速度由表达式本身确定的动画。例如，假设您想要一个层从零到200%的比例增加在很短的时间段，然后冲过一点点，并定居在200%。所以动画触发器的层的在一点上，我们会对其进行设置。这里有一个基本的表达，将图层从规模0到100%超过十分之一秒，开始在一层的分析：

　　t = time - inPoint;

　　startVal = [0,0];

　　endVal = [200,200];

　　dur = 0.1;

　　linear(t,0,dur,startVal,endVal);

[Ok3w_NextPage]

　　计算缓冲

　　现在，我们将添加一些超调。在这种情况下，由于进入的动画是通过一个linear()函数生成，我们可以很容易地计算速度进入过冲。事实证明，该速度是刚结束值减去开始值，由持续时间，在这种情况下将是分割(endVal - startVal)/dur。因此，我们需要修改规模化表达，使其持续上升直到它达到endVal，然后切换到超调振荡。最终的表达式如下所示：

　　freq = 3;

　　decay = 5;t = time - inPoint;

　　startVal = [0,0];

　　endVal = [200,200];

　　dur = 0.1;

　　if (t < dur){

　　linear(t,0,dur,startVal,endVal);

　　}else{

　　amp = (endVal - startVal)/dur;

　　w = freq*Math.PI*2;

　　endVal + amp*(Math.sin((t-dur)*w)/Math.exp(decay*(t-dur))/w);

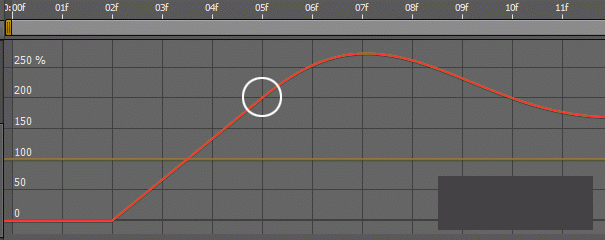
　　请注意，从linear()坡道的过冲振荡(其中发生在5f)的过渡完美匹配。

　　缓冲动画匹配传入动画的速度。

　　诀窍使这两个动画比赛的速度就是神秘的可变瓦特这里，w表示角速度振荡。没有进入很多细节，事实证明，除以输入速度与角速度的振荡给出了一个匹配完美的超调。具体而言，这意味着更高的振荡频率越低，产生的过冲的幅度。记得有过冲的一个重要的事情是，你没有直接控制超调幅度(放大器变量由下式计算)。如果你想有一个较大的超调，你或者需要增加进来的速度，或者减少其振荡频率。这是值得摆弄表情看频率，传入速度，并导致超调幅度之间的相互作用。

　　这是一个非常有用的和通用的表达。这里有好玩的，你可以使用文本图层来获取文本字符，随机从零到100%的比例增加，有超调的变化。为了得到这个工作，你想补充一个动画缩放你的文字层，缩放值设置为百分之零，添加表达式选择器，(那么你可以删除范围选择)，最后，更换式的默认表情选择的物业数量与此：

　　freq = 3;

　　decay = 5;

　　maxDelay = 1.0;seedRandom(textIndex,true);

　　myDelay = random(maxDelay);

　　t = time - (inPoint + myDelay);

　　startVal = [100,100];

　　endVal = [0,0];

　　dur = 0.1;

　　if (t < dur){

　　linear(t,0,dur,startVal,endVal);

　　}else{

　　amp = (endVal - startVal)/dur;

　　w = freq*Math.PI*2;

　　endVal + amp*(Math.sin((t-dur)*w)/Math.exp(decay*(t-dur))/w);

　　}

　　这里是你可以用它来获得文字层的3D人物依次摆成视图冲另一种变体。 你会发现，这和以前版本的表达之间的唯一真正的区别是计算基于角色的textIndex值随机延迟变量(myDelay)的线。使用textIndex作为随机种子，确保每个角色都会获得一个独特的，随机延迟。在这里，过冲表达已结合随机文本缩放。

　　首先，你需要你的文字层的锚点移动到文本的顶部。你可以用一个锚点动画做到这一点。此外，请确保您已启用每个字符3D。添加一个新的动画为旋转(不使用你用来调整锚点是同一个)。设置X旋转，使得文本(垂直于屏幕)旋转出的角度值。添加表达式选择和删除功能选择。更换表达选择的财产金额与此默认的表达式：

[Ok3w_NextPage]

　　freq = 2;

　　decay = 5;

　　delay = .15;

　　dur = .12;myDelay = (textIndex-1)*delay;

　　t = time - (inPoint + myDelay);

　　startVal = 100;

　　endVal = 0;if(t < dur){

　　linear(t,0,dur,startVal,endVal);

　　}else{

　　amp = (endVal - startVal)/dur;

　　w = freq*Math.PI*2;

　　endVal + amp*(Math.sin(t*w)/Math.exp(decay*t)/w);

　　}

　　3D人物旋转到顺序来看，有缓冲。

　　关键帧缓冲

　　或许是一种较为普遍的超调的应用将增加超调，以一个关键帧动画。这实际上是相当简单的，因为表达式语言，您可以访问属性的速度。在这种情况下，我们将使用velocityAtTime()函数来获得进入的速度在最近的关键帧。这是关键帧冲表达式：

　　freq = 3;

　　decay = 5;n = 0;

　　if (numKeys > 0){

　　n = nearestKey(time).index;

　　if (key(n).time > time) n--;

　　}

　　if (n > 0){

　　t = time - key(n).time;

　　amp = velocityAtTime(key(n).time - .001);

　　w = freq*Math.PI*2;

　　value + amp*(Math.sin(t*w)/Math.exp(decay*t)/w);

　　}else

　　value

　　与以前一样，前两行只定义控制振荡的频率和衰减的变量。接下来的部分是一个方便的小程序，发现最新的关键帧。表达的其余部分提取属性的速度在那个关键帧并使用该速度作为计算过冲的幅度。需要注意的是表达实际获取速度的关键帧之前0.001秒，以确保它拿起传入的(而不是传出)的速度。

　　其中该表达的非常好的特点是，它是property-agnostic无关的，这意味着它应该工作，原样，具有可关键帧几乎所有的property-agnostic。看到两个栏的电影动画关键帧的两个例子，其中的表达提供过冲。首先演示了一个流行的X旋转过冲，其中层关键帧以快速旋转100度至零，以表达提供超调动画。第二个演示过冲应用于关键帧的位置属性。

　　弹跳的表达已经被应用到了关键帧的X轴旋转性能。

　　

　　这里，缓冲表达已施加到关键帧位置属性。

　　弹跳概述

　　我们的最终目标是在这里要结束了，将模拟反弹在关键帧运动结束的表达。要了解一个反弹仿真工作，虽然，这是非常有用开始与一个场景，可能是比较熟悉的，一个弹丸的反弹，当它击中地面/地板。为了让事情简单，我们将其限制为两个维度。当启动一个2D弹丸，有若干在起作用的因素：在重力的作用，对象的弹性，发射角度，初始速度，有时摩擦。模拟这种运动的表达基本上具有分裂初始速度到x和y分量。重力工作在y方向上。在每个弹跳，对象失去根据基于所述摩擦的弹性以及x速度ÿ速度。考虑到所有这些因素考虑进去给你的2D反弹，看起来像这样的表达式：

　　elev = degreesToRadians(75);

　　v = 1900;

　　e = .7;

　　f = .5;

　　g = 5000;

　　nMax = 9;

　　tLaunch = 1;

　　vy = v*Math.sin(elev);

　　vx = v*Math.cos(elev);

　　if (time >= tLaunch){

[Ok3w_NextPage]

　　t = time - tLaunch;

　　tCur = 0;

　　segDur = 2*vy/g;

　　tNext = segDur;

　　d = 0; // x distance traveled

　　nb = 0; // number of bounces

　　while (tNext < t && nb <= nMax){

　　d += vx*segDur;

　　vy *= e;

　　vx *= f;

　　segDur *= e;

　　tCur = tNext;

　　tNext += segDur;

　　nb++

　　}

　　if(nb <= nMax){

　　delta = t - tCur;

　　x = d + delta*vx;

　　y = delta*(vy - g*delta/2);

　　}else{

　　x = d;

　　y = 0;

　　}

　　value + [x,-y]

　　}else

　　value

　　有几件事情需要注意的这一表达。弹跳参数发射角(海拔)，初始速度(ⅴ)，弹性(e)所示，摩擦(f)和比重(g)-are所有限定在表达的顶部。请注意，您还必须定义，以保持从表情到消失的小反弹无尽计算反弹(n最大)的最大数量。这个版本的表达还包括一个变量来控制发射时间(tLaunch)。

　　二维模拟反弹使用发射角度，初速度，重力，弹力，和摩擦。

　　关键帧反弹

　　现在，我们来看看这样的论点：这确实是本节的点。该表达式使用属性的速度进入一个关键帧来计算一个反弹(方向相反的到传入动画)的一系列减少反弹的。表达式使用大部分逻辑从基本2D弹跳表达，所不同的是，没有必要担心发射角和初始速度(那些从关键帧中检索)，或磨擦。这种表达已经用老式大多数属性的工作。见边栏为影片加在规模，位置(2D和3D)，并且旋转属性的例子。这里的表达式：

　　e = .7;

　　g = 5000;

　　nMax = 9;n = 0;

　　if (numKeys > 0){

　　n = nearestKey(time).index;

　　if (key(n).time > time) n--;

　　}

　　if (n > 0){

　　t = time - key(n).time;

　　v = -velocityAtTime(key(n).time - .001)*e;

　　vl = length(v);

　　if (value instanceof Array){

　　vu = (vl > 0) ? normalize(v) : [0,0,0];

　　}else{

　　vu = (v < 0) ? -1 : 1;

　　}

　　tCur = 0;

　　segDur = 2*vl/g;

　　tNext = segDur;

　　nb = 1; // number of bounces

　　while (tNext < t && nb <= nMax){

　　vl *= e;

　　segDur *= e;

　　tCur = tNext;

　　tNext += segDur;

　　nb++

　　}

　　if(nb <= nMax){

　　delta = t - tCur;

　　value + vu*delta*(vl - g*delta/2);

　　}else{

　　value

　　}

　　}else

　　value

　　该弹回表达应用于位置，旋转和缩放属性。

　　和以前一样，你可以通过调整弹性(E)和重力(G)变量控制反弹的特点。